The paper introduces a new global log-bilinear regression model that combines the advantages of the two major model families in the literature: global matrix factorization and local context window methods. The model efficiently leverages statistical information by training only on the nonzero elements in a word-word co-occurrence matrix. The model produces a vector space with meaningful sub-structure, as evidenced by its performance of 75% on a recent word analogy task. It also outperforms related models on similarity tasks and named entity recognition.
The GloVe Model
Using the insights a new model is constructed for word representation which is called GloVe, for Global Vectors, because the global corpus statistics are captured directly by the model.
First we establish some notation. Let the matrix of word-word co-occurrence counts be denoted by X, whose entries Xᵢⱼ tabulate the number of times word j occurs in the context of word i. Let Xᵢ = ∑kXᵢk be the number of times any word appears in the context of word i. Finally, let Pᵢⱼ = P(j|i) = Xᵢⱼ / Xᵢ be the probability that word j appear in the context of word i.
For example consider two words i and j that exhibit a particular aspect of interest; for concreteness, suppose we are interested in the concept of thermodynamics phase, for which we might take i = ice and j = steam. The relationship of these words can be examined by studying the ration of their co-occurrence probabilities with various probe words, k. For words related to ice but not steam, say k = solid, we expect the ratio Pᵢk / Pjk will be large. Similarly, for words k related to ice but not steam, say k = gas, the ratio should be small. For words k like water or fashion, that are either related to both ice and steam, or to neither, the ratio should be close to one.
The appropriate starting point for word vector learning should be with ratio of co-occurrence probabilities. Noting that the ratio PikPjk depends on three words /i , j and k, the most general model takes the form,
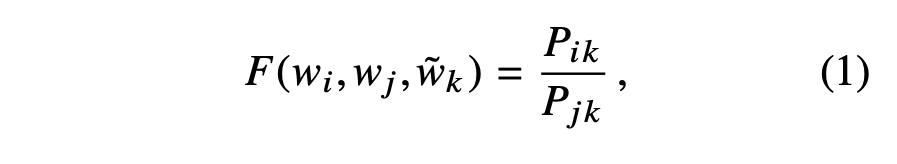
where w ∈ Rd and word vectors and w ∈ Rd are separate context word vectors. We can restrict out consideration to those functions F that depend only on the difference of the two target words, modifying Eqn.(1) to,
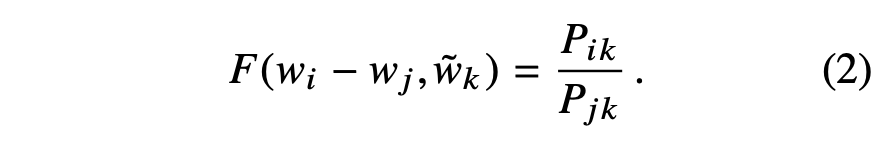
The argument of F in Eqn.(2) are vectors while the right-hand side is a scalar.
We can take the dot product of the arguments which prevents F from mixing the vector dimension in undesirable ways.
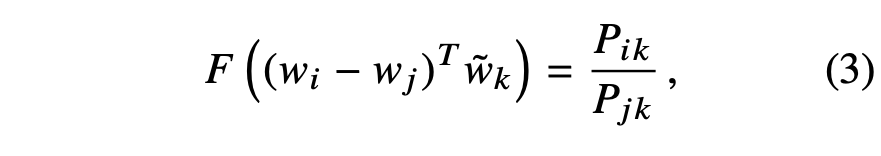
Next, note that for word-word co-occurrence matrices, the distinction between a word and a context word is arbitrary and that we are free to exchange the two roles. To do so consistently, we must not only exchange w ↔ w˜ but also X ↔ X T . Our final model should be invariant under this relabeling, but Eqn. (3) is not. However, the symmetry can be restored in two steps. First, we require that F be a homomorphism between the groups (R,+) and (R>0, ×), i.e.,
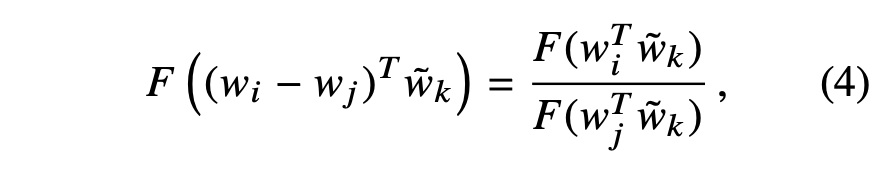
which, by Eqn. (3), is solved by,
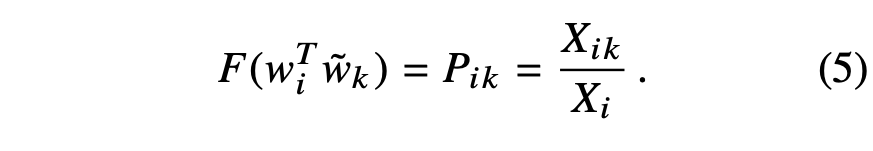
The solution to Eqn. (4) is F = exp, or,
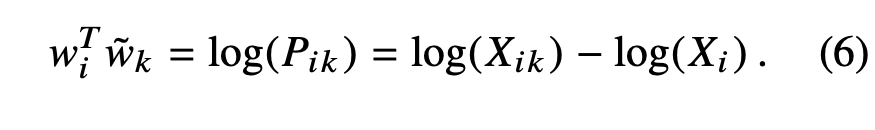
Next, we note that Eqn. (6) would exhibit the exchange symmetry if not for the log(Xi) on the right-hand side. However, this term is independent of k so it can be absorbed into a bias bi for wi . Finally, adding an additional bias b˜ k for ˜wk restores the symmetry,
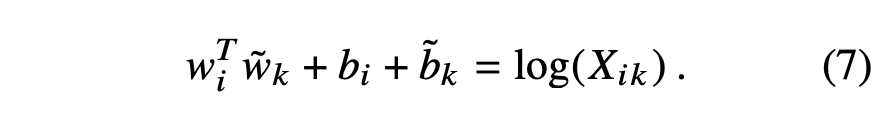
Eqn. (7) is a drastic simplification over Eqn. (1), but it is actually ill-defined since the logarithm diverges whenever its argument is zero. One resolution to this issue is to include an additive shift in the logarithm, log(Xik) → log(1 + Xik ), which maintains the sparsity of X while avoiding the divergences. A main drawback to this model is that it weighs all co-occurrences equally, even those that happen rarely or never.
We propose a new weighted least squares regression model that addresses these problems. Casting Eqn. (7) as a least squares problem and introducing a weighting function f (Xij) into the cost function gives us the model
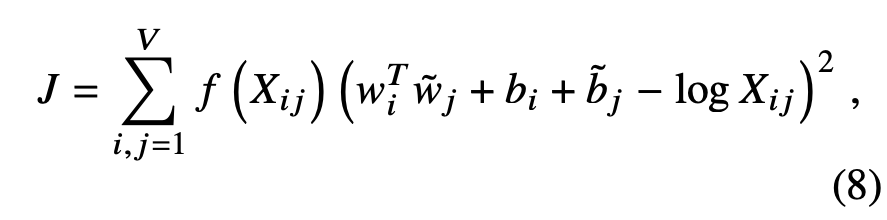
where V is the size of the vocabulary. The weighting function should obey the following properties:
- f (0) = 0. If f is viewed as a continuous function, it should vanish as x → 0 fast enough that the limx→0 f (x) log2 x is finite.
- f (x) should be non-decreasing so that rare co-occurrences are not overweighted.
- f (x) should be relatively small for large values of x, so that frequent co-occurrences are not overweighted.
The performance of the model depends weakly on the cutoff, which we fix to xmax = 100 for all our experiments. We found that α = 3/4 gives a modest improvement over a linear version with α = 1. As can be seen from Eqn. (8) and the explicit form of the weighting function f (X), the computational complexity of the model depends on the number of nonzero elements in the matrix X. As this number is always less than the total number of entries of the matrix, the model scales no worse than O(|V | ²).
Disclosure
Most of the things are directly from the paper. This post is meant to be a one place for all the papers that I read and take notes. Read the original paper here.