The paper presents a general end-to-end approach to sequence learning that makes minimal assumptions on the sequence structure. The method uses a multilayered Long Short-Term Memory (LSTM) to map the input sequence to a vector of fixed dimensionality, and then another LSTM to decode the target sequence from the vector. A Straightforward application of the Long Short-Term Memory (LSTM) architecture can solve general sequence to sequence problems. The idea is to use one LSTM to read the input sequence, one timestep at a time, to obtain a large fixed-dimensional vector representation, and then another LSTM to extract the output sequence from that vector. The Second LSTM is essentially a recurrent neural network language model except that it is conditioned on the input sequence. The LSTM’s ability to successfully learn on data with long range temporal dependencies makes it a natural choice for this application due to the considerable time lag between the inputs and their corresponding outputs.
The Model
The goal of the LSTM is to estimate the conditional probability p(y1,…yT’∣x₁,…xT) where (x₁,…xT) is an input sequence and y₁,…yT’ is its corresponding output sequence whose length T’ may differ from T. The LSTM computes this conditional probability by first obtaining the fixed-dimensional representation v of the input sequence (x₁,…xT) given by the last hidden state of the LSTM, and then computing the probability of y₁,…yT` with standard LSTM-LM formulation whose initial hidden state is set to the representation v of x₁,…xT :
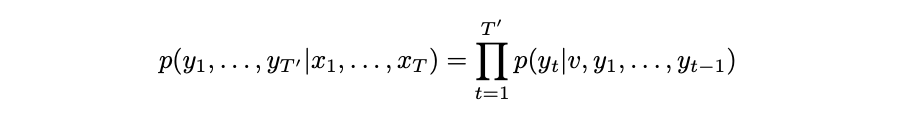
In this equation, each p(yt|v, y₁, . . . , yt−1) distribution is represented with a softmax over all the words in the vocabulary. Note that we require that each sentence ends with a special end-of-sentence symbol
- First, two different LSTMs were used: one for the input sequence and another for the output sequence, because doing so increases the number model parameters at negligible computational cost and makes it natural to train the LSTM on multiple language pairs simultaneously.
- Second, it was found that deep LSTMs significantly outperformed shallow LSTMs, so an LSTM with four layers was chosen.
- Third, it was found that it is extremely valuable to reverse the order of the words of the input sentence. So for example, instead of mapping the sentence a, b, c to the sentence α, β, γ, the LSTM is asked to map c, b, a to α, β, γ, where α, β, γ is the translation of a, b, c. This way, a is in close proximity to α, b is fairly close to β, and so on, a fact that makes it easy for SGD to “establish communication” between the input and the output. We found this simple data transformation to greatly improve the performance of the LSTM.
Takeaways
- A useful property of the LSTM is that it learns to map an input sentence of variable length into a fixed-dimensional vector representation.
- The model is aware of word order and is fairly invariant to the active and passive voice.
- LSTM learns much better when the source sentences are reversed (the target sentences are not reversed).
- LSTM trained on reversed source sentences did much better on long sentences that LSTMs trained on the raw source sentences, which suggests that reversing the input sentences results in LSTMs with better memory utilization.
- A large deep LSTM, that has a limited vocabulary and that makes almost no assumption about problem structure can outperform a standard SMT-based system whose vocabulary is unlimited on a large-scaled MT task.
Disclosure
Most of the things are directly from the paper. This post is meant to be a one place for all the papers that I read and take notes. Read the original paper here.