The paper introduces a new RNN variant that uses multiplicative (or “gated”) connections which allow the current input character to determine the transition matrix from one hidden state vector to the next. The goal of the paper is to demonstrate the power of large RNNs trained with the new Hessian-Free optimizer by applying them to the task of predicting the next character in a stream of text. “MRNN” architecture uses multiplicative connections to allow the current input character to determine the hidden-to-hidden weight matrix.
The Tensor RNN
The dynamics of the RNN’s hidden states depend on the hidden-to-hidden matrix and on the inputs. In a standard RNN, the current input xt is first transformed via the visible-to-hidden weight matrix Whx and then contributes additively to the input for the current hidden state. A more powerful way for the current input character to affect the hidden state dynamics would be to determine the entire hidden-to-hidden matrix (which de- fines the non-linear dynamics) in addition to providing an additive bias.
For example, the character string “ing” is quite probable after “fix” and also quite probable after “break”. If the hidden state vectors that represent the two histories “fix” and “break” share a common representation of the fact that this could be the stem of a verb, then this common representation can be acted upon by the character “i” to produce a hidden state that predicts an “n”. For this to be a good prediction we require the conjunctionof the verb-stem representation in the previous hidden state and the character “i”. One or other of these alone does not provide half as much evidence for predicting an “n”: It is their conjunction that is important. This strongly suggests that we need a multiplicative interaction. To achieve this goal we modify the RNN so that its hidden- to-hidden weight matrix is a (learned) function of the current input xt:
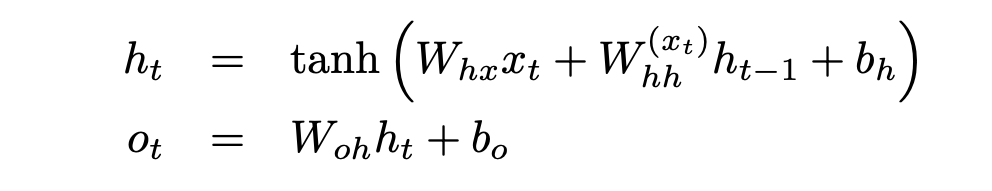
This allows each character to specify a different hidden-to-hidden weight matrix.
It is natural to define W(xt)hh using a tensor. If we store M matrices, W1hh,…,W(M)hh , where M is the number of dimensions of xt, we could define W(xt)hh by the equation
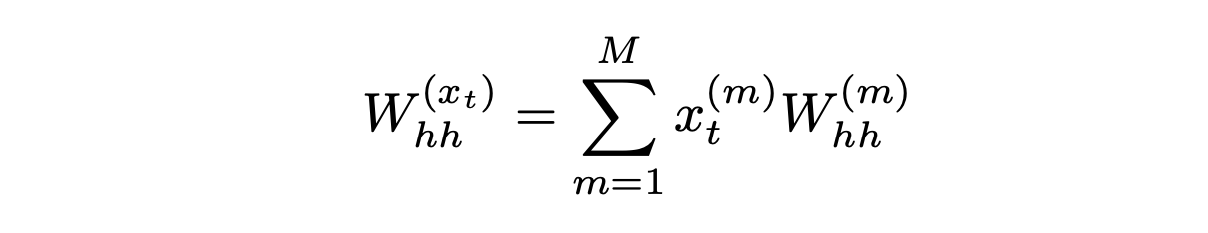
where x(m)t is the m-th coordinate of xt. When the input xt is a 1-of-M encoding of a character, it is easily seen that every character has an associated weight matrix and W(xt)hh is the matrix assigned to the character represented by xt.
The Multiplicative RNN (MRNN)
The above scheme, while appealing, has a major drawback: Fully general 3-way tensors are not practical because of their size. In particular, if we want to use RNNs with a large number of hidden units (say, 1000) and if the dimensionality of xt is even moderately large, then the storage required for the tensor W(xt)hh becomes prohibitive.
It turns out we can remedy the above problem by factoring the tensor W (xt)hh. This is done by introducing the three matrices Wfx , Whf , and Wfh, and reparameterizing the matrix W(xt)hh by the equation
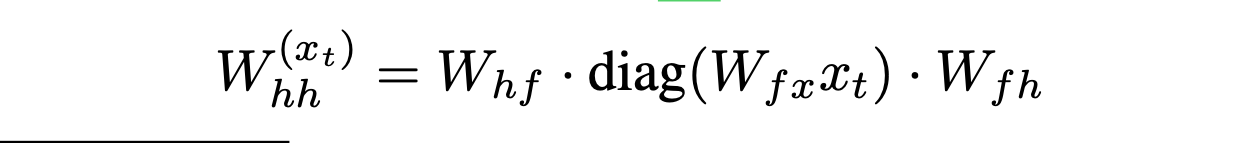
The Multiplicative RNN (MRNN) is the result of factorizing the Tensor RNN. The MRNN computes the hidden state sequence (h1 , . . . , hT ), an additional “factor state sequence” (f1 , . . . , fT ), and the output sequence (o1 , . . . , oT ) by iterating the equations
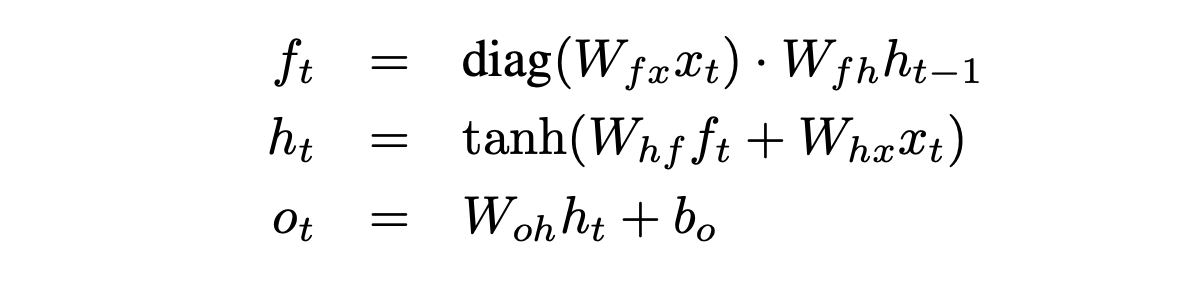
The tensor factorization has the interpretation of an additional layer of multiplicative units between each pair of consecutive layers, so the MRNN actually has two steps of nonlinear processing in its hidden states for every input timestep. Each of the multiplicative units outputs the value ft which is the product of the outputs of the two linear filters connecting the multiplicative unit to the previous hidden states and to the inputs.
The Result
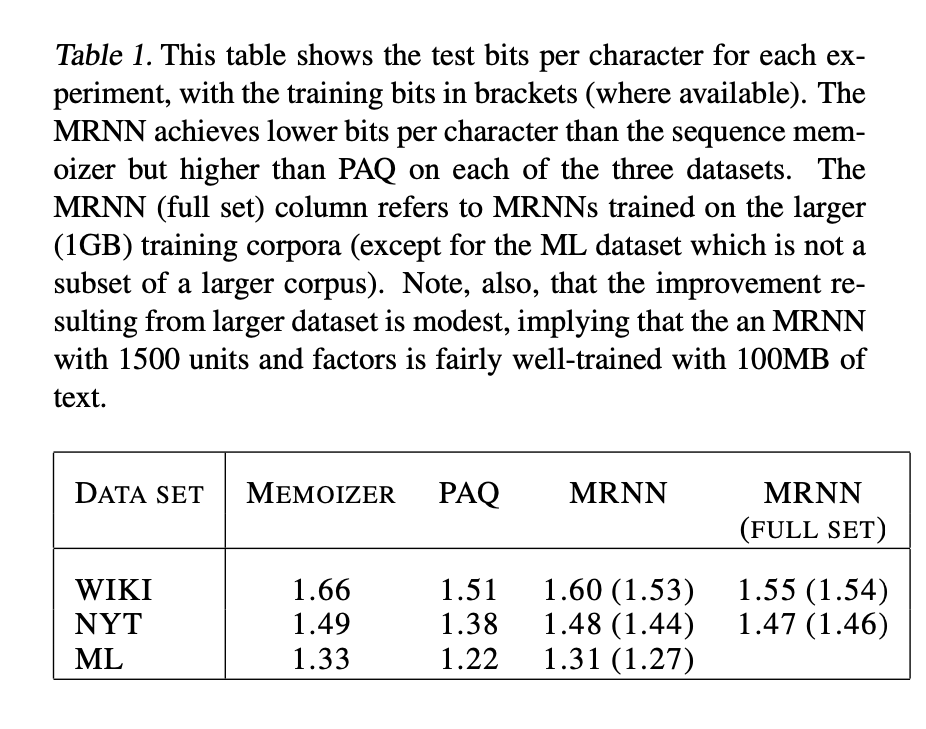
The MRNN predicts the test set more accurately than the sequence memoizer but less accurately than the dictionary-free PAQ on the three datasets.
Disclosure
Most of the things are directly from the paper. This post is meant to be a one place for all the papers that I read and take notes. You can read the paper in its entirety here.